To enable purchasers to compare commercially available instruments and evaluate new instrument designs, quantitative criteria for the performance of instruments are needed. These criteria must clearly specify how well an instrument measures the desired input and how much the output depends on interfering and modifying inputs. Characteristics of instrument performance are usually subdivided into two classes on the basis of the frequency of the input signals.
Static characteristics describe the performance of instruments for dc or very low frequency inputs. The properties of the output for a wide range of constant inputs demonstrate the quality of the measurement, including nonlinear and statistical effects. Some sensors and instruments, such as piezoelectric devices, respond only to time-varying inputs and have no static characteristics.
Dynamic characteristics require the use of differential and/or integral equations to describe the quality of the measurements. Although dynamic characteristics usually depend on static characteristics, the nonlinearities and statistical variability are usually ignored for dynamic inputs, because the differential equations become difficult to solve. Complete characteristics are approximated by the sum of static and dynamic characteristics. This necessary oversimplification is frequently responsible for differences between real and ideal instrument performance.
Here we will talk regarding the static characteristics of a Biomedical Instrument
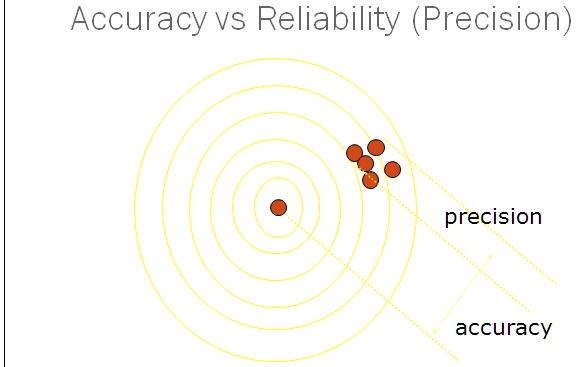
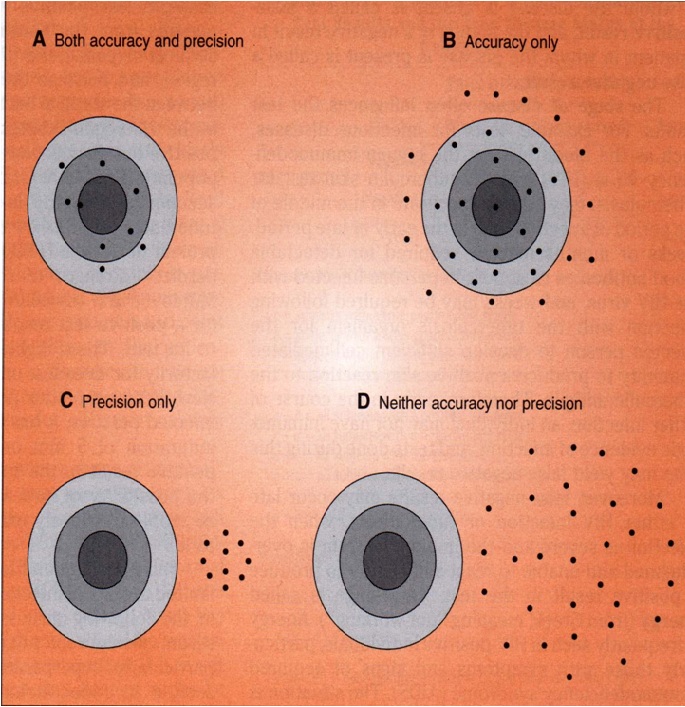
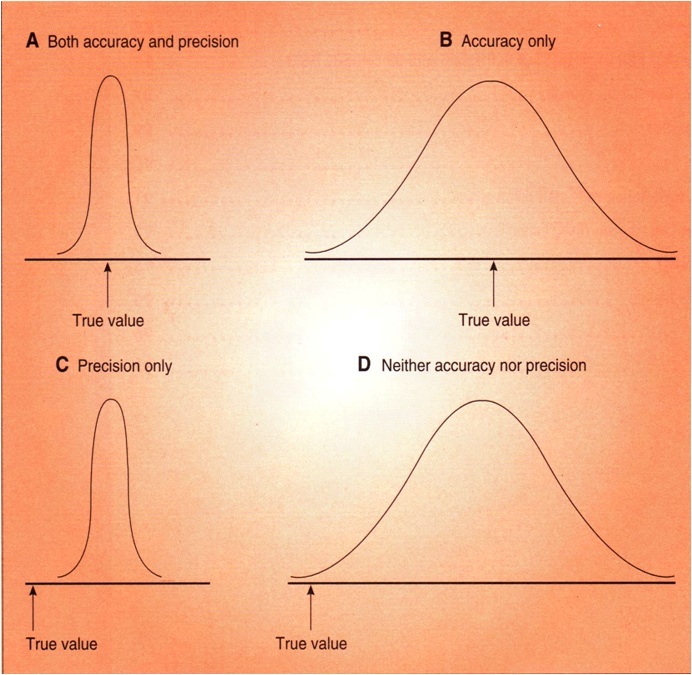
ACCURACY
The accuracy of a single measured quantity is the difference between the true value and the measured value divided by the true value. This ratio is usually expressed as a percent. Because the true value is seldom available, theaccepted true value or reference value should be traceable to the National Institute of Standards and Technology. The accuracy usually varies over the normal range of the quantity measured, usually decreases as the full-scale value of the quantity decreases on a multirange instrument, and also often varies with the frequency of desired, interfering, and modifying inputs. Accuracy is a measure of the total error without regard to the type or source of the error. The possibility that the measurement is low and that it is high are assumed to be equal. The accuracy can be expressed as percent of reading, percent of full scale, (+/-)number of digits for digital readouts, or (+/-)1/2 the smallest division on an analog scale. Often the accuracy is expressed as a sum of these, for example, on a digital device, (+/-)0.01% of reading (+/-)0.015% of full-scale (+/-)1 digit. If accuracy is expressed simply as a percentage, full scale is usually assumed. Some instrument manufacturers specify accuracy only for a limited period of time.
PRECISION
The precision of a measurement expresses the number of distinguishablealternatives from which a given result is selected. For example, a meter that displays a reading of 2.434 V is more precise than one that displays a reading of 2.43 V. High-precision measurements do not imply high accuracy, however, because precision makes no comparison to the true value.
RESOLUTION
The smallest incremental quantity that can be measured with certainty is the resolution. If the measured quantity starts from zero, the term threshold is synonymous with resolution. Resolution expresses the degree to which nearly equal values of a quantity can be discriminated.’
REPRODUCIBILITY
The ability of an instrument to give the same output for equal inputs applied over some period of time is called reproducibility or repeatability. Reproducibility does not imply accuracy. For example, a broken digital clock with an AMor PM indicator gives very reproducible values that are accurate only once a day.
STATISTICAL CONTROL
The accuracy of an instrument is not meaningful unless all factors, such as the environment and the method of use, are considered. Statistical control ensures that random variations in measured quantities that result from all factors that influence the measurement process are tolerable. Any systematic errors or bias can be removed by calibration and correction factors, but random variations pose a more difficult problem. The measurand and/or the instrument may introduce statistical variations that make outputs unreproducible. If the cause of this variability cannot be eliminated, then statistical analysis must be used to determine the error variation. Making multiple measurements and averaging the results can improve the estimate of the true value.